Teorema de Circuitos Electricos

SUPERPOSICIÓN DE FUENTES

El teorema de superposición sólo se puede utilizar en el caso de circuitos eléctricos lineales, es decir circuitos formados únicamente por componentes lineales (en los cuales la amplitud de la corriente que los atraviesa es proporcional a la amplitud de voltaje a sus extremidades).

El teorema de superposición ayuda a encontrar:

Valores de voltaje, en una posición de un circuito, que tiene más de una fuente de voltaje.
Valores de corriente, en un circuito con más de una fuente de voltaje.

Este teorema establece que el efecto que dos o más fuentes tienen sobre una impedancia es igual, a la suma de cada uno de los efectos de cada fuente tomados por separado, sustituyendo todas las fuentes de voltaje restantes por un corto circuito, y todas las fuentes de corriente restantes por un circuito abierto.

En el circuito de arriba de la figura de la izquierda, calculemos el voltaje en el punto A utilizando el teorema de superposición.Como hay dos generadores, hay que hacer dos cálculos intermedios.

En el primer cálculo, conservamos la fuente de voltaje de la izquierda y remplazamos la fuente de corriente por un circuito abierto. El voltaje parcial obtenido es::

V_1=V_\circ\textstyle{{Z_2\over Z_1+Z_2}}

En el segundo cálculo, guardamos la fuente de corriente de derecha y remplazamos la fuente de voltaje por un cortocircuito. El voltaje obtenido es::

V_2=I_\circ \left(Z_1\parallel Z_2\right)= I_\circ \textstyle{{Z_1Z_2\over Z_1+Z_2}}

El voltaje que buscamos es la suma de los dos voltajes parciales::

V_A=V_1+V_2=V_\circ \textstyle{{Z_2\over Z_1+Z_2}}+ I_\circ \textstyle{{Z_1Z_2\over Z_1+Z_2}}= \textstyle{{V_\circ Z_2+I_\circ Z_1Z_2\over Z_1+Z_2}}

TRANSFORMACIÓN DE FUENTES

Se pueden intercambiar fuentes prácticas de voltaje o corriente sin afectar al resto del circuito.

Para transformar una fuente práctica de voltaje en una fuente práctica de corriente se calcula la corriente de la fuente ideal como

Y se conecta en paralelo con una resistencia Rs.

Para transformar una fuente práctica de corriente en una fuente práctica de voltaje se calcula el voltaje de la fuente ideal como

Y se conecta en serie con una resistencia Rs.

EJEMPLO

Calcular IL en la fuente práctica de corriente
Transformar la fuente práctica de corriente en una fuente práctica de voltaje
Calcule IL si RL = 80Ω en la fuente práctica de voltaje
Calcule la potencia suministrada por la fuente ideal en cada caso
¿Qué valor de RL absorberá la máxima potencia?
¿Cuál es el valor de la potencia máxima?

Solución:

1. Cálculo de IL: se usa un divisor de corriente.

2. Transformación en una fuente práctica de voltaje

3. Cálculo de IL

4. Cálculo de la potencia suministrada por la fuente ideal en cada caso.

5. ¿Qué valor de RL absorberá la máxima potencia?

RL = Rs

RL = 2o Ω

6. ¿Cuál es el valor de la potencia máxima?

Transformación de Fuentes

TEOREMA DE THEVENIN Y NORTON

1. Teorema de Thevenin

Cualquier red compuesta por resistores lineales, fuentes independientes y fuentes dependientes, puede ser sustituida en un par de nodos por un circuito equivalente formado por una sola fuente de voltaje y un resistor serie.

Por equivalente se entiende que su comportamiento ante cualquier red externa conectada a dicho par de nodos es el mismo al de la red original (igual comportamiento externo, aunque no interno).

La resistencia se calcula anulando las fuentes independientes del circuito (pero no las dependientes) y reduciendo el circuito resultante a su resistencia equivalente vista desde el par de nodos considerados. Anular las fuentes de voltaje equivale a cortocircuitarlas y anular las de corriente a sustituirlas por un circuito abierto.

El valor de la fuente de voltaje es el que aparece en el par de nodos en circuito abierto.

2. Teorema de Norton

Cualquier red compuesta por resistores lineales, fuentes independientes y fuentes dependientes puede ser sustituida, en un par de nodos, por un circuito equivalente formado por una sola fuentes de corriente y un resistor en paralelo.

La resistencia se calcula (igual que para el equivalente de Thevenin) anulando las fuentes independientes del circuito (pero no las dependientes) y reduciendo el circuito resultante a su resistencia equivalente vista desde el par de nodos considerados.

El valor de la fuente de corriente es igual a la corriente que circula en un cortocircuito que conecta los dos nodos.

TEOREMA DE MÁXIMA TRANSFERENCIA DE POTENCIA

El teorema de máxima transferencia de potencia establece que, dada una fuente, con una resistencia de fuente fijada de antemano, la resistencia de carga que maximiza la transferencia de potencia es aquella con un valor óhmico igual a la resistencia de fuente. También este ayuda a encontrar el teorema de Thevenin y Norton.

El teorema establece cómo escoger (para maximizar la transferencia de potencia) la resistencia de carga, una vez que la resistencia de fuente ha sido fijada, no lo contrario. No dice cómo escoger la resistencia de fuente, una vez que la resistencia de carga ha sido fijada. Dada una cierta resistencia de carga, la resistencia de fuente que maximiza la transferencia de potencia es siempre cero, independientemente del valor de la resistencia de carga.

Se dice que Moritz von Jacobi fue el primero en descubrir este resultado, también conocido como "Ley de Jacobi".

El teorema fue originalmente malinterpretado (notablemente por Joule) para sugerir que un sistema que consiste de un motor eléctrico comandado por una batería no podría superar el 50% de eficiencia pues, cuando las impedancias estuviesen adaptadas, la potencia perdida como calor en la batería sería siempre igual a la potencia entregada al motor. En 1880, Edison (o su colega Francis Robbins Upton) muestra que esta suposición es falsa, al darse cuenta que la máxima eficiencia no es lo mismo que transferencia de máxima potencia. Para alcanzar la máxima eficiencia, la resistencia de la fuente (sea una batería o un dínamo) debería hacerse lo más pequeña posible. Bajo la luz de este nuevo concepto, obtuvieron una eficiencia cercana al 90% y probaron que el motor eléctrico era una alternativa práctica al motor térmico.

Potencia transferida en función de la adaptación. Solo se tiene en cuenta la parte resistiva. Se supone que las reactancias están compensadas.

En esas condiciones la potencia disipada en la carga es máxima y es igual a:

P_\mathrm{max}=\textstyle{V^2\over 4 R_g}

La condición de transferencia de máxima potencia no resulta en eficiencia máxima. Si definimos la eficiencia

\scriptstyle{\eta}

como la relación entre la potencia disipada por la carga y la potencia generada por la fuente, se calcula inmediatamente del circuito de arriba que

\eta = {R_\mathrm{c} \over {R_\mathrm{c} + R_\mathrm{g} } } = { 1 \over { 1 + { R_\mathrm{g} \over R_\mathrm{c} } } }

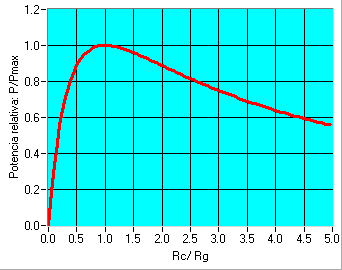
La eficiencia cuando hay adaptación es de solo 50%. Para tener eficiencia máxima, la resistencia de la carga debe ser infinitamente más grande que la resistencia del generador. Por supuesto en ese caso la potencia transferida tiende a cero. Cuando la resistencia de la carga es muy pequeña comparada a la resistencia del generador, tanto la eficiencia como la potencia transferida tienden a cero. En la curva de la derecha hemos representado la potencia transferida relativa a la máxima posible (cuando hay adaptación) con respecto al cociente entre la resistencia de carga y la del generador. Se supone que las reactancias están compensadas completamente. Nótese que el máximo de la curva no es crítico. Cuando las dos resistencias están desadaptadas de un factor 2, la potencia transferida es aún 89% del máximo posible.

Cuando la impedancia de la fuente es una resistencia pura (sin parte reactiva), la adaptación se hace con una resistencia y es válida para todas las frecuencias. En cambio, cuando la impedancia de la fuente tiene una parte reactiva, la adaptación solo se puede hacer a una sola frecuencia. Si la parte reactiva es grande (comparada a la parte resistiva), la adaptación será muy sensible a la frecuencia, lo que puede ser un inconveniente.